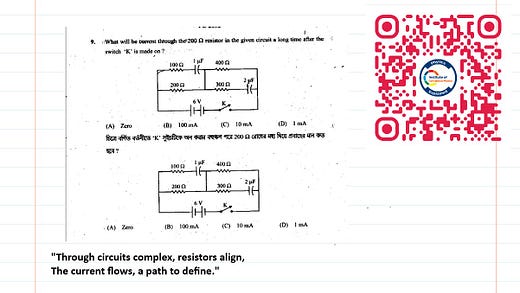
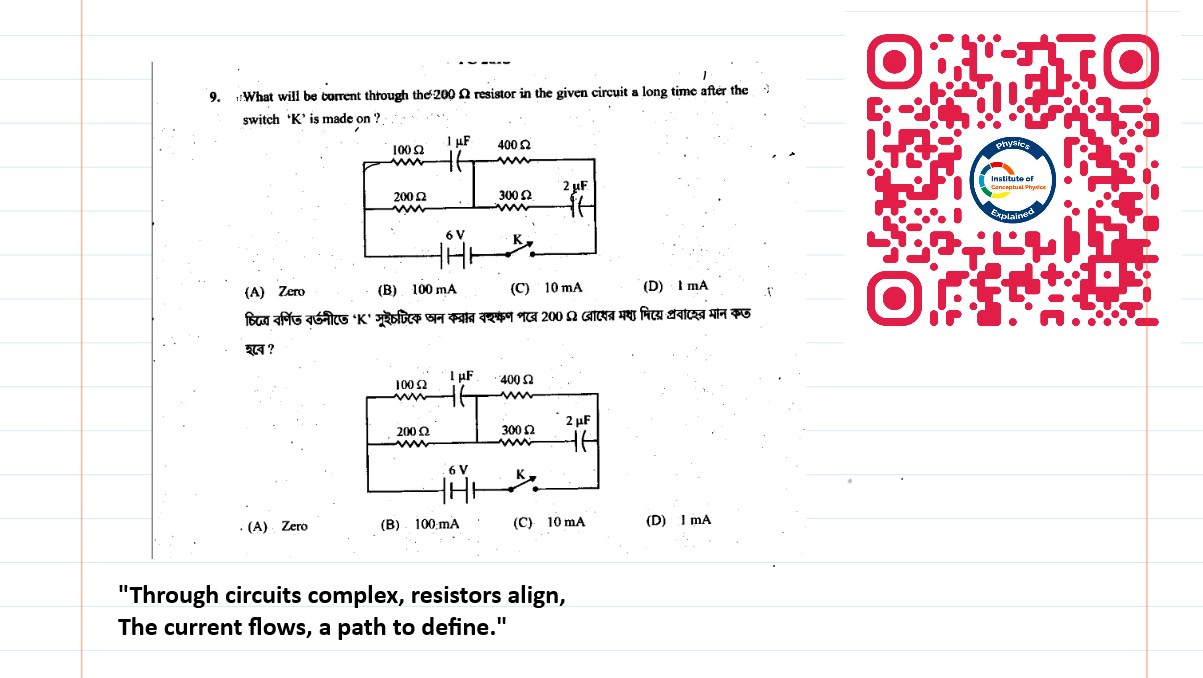
Mastering DC Circuits: Solving Resistor-Capacitor Networks in Steady State"

Physics Explained for NEET, WBJEE, VITEE, BITSAT, JEE mains, APEAMCET-Sample Video Included

To solve direct current (DC) circuits that include resistors and capacitors, where the capacitor has been connected for a long time, follow these steps:

Key Concept: Capacitor Behavior in a DC Circuit

• Steady State: After a long time (in the context of a DC circuit), the capacitor is fully charged, and no current flows through it. The capacitor behaves like an open circuit (infinite resistance) in steady state.

---

Steps to Solve the Circuit

1. Redraw the Circuit for Steady State:

   • Replace the capacitor with an open circuit.

   • This eliminates any current through the branch containing the capacitor.

2. Simplify the Circuit:

   • Analyze the resulting circuit, which now consists only of resistors and possibly voltage sources.

   • Use series and parallel resistor combinations to simplify the circuit.

3. Apply Kirchhoff’s Laws (if necessary):

   • Kirchhoff's Current Law (KCL): The total current entering a junction equals the total current leaving it.

   • Kirchhoff's Voltage Law (KVL): The sum of potential differences in a closed loop is zero.

4. Calculate Circuit Parameters:

   • Determine currents and voltages across the resistors using Ohm’s Law: V=IR

5. Determine the Capacitor Voltage:

   • The voltage across the capacitor in steady state is equal to the voltage across the branch where it is connected.

---

Example Problem

Circuit: A DC source of VVV volts is connected to a resistor R1, and a capacitor C is in parallel with another resistor R2

Solution:

1. Steady-State Behavior:

   • The capacitor is fully charged and behaves like an open circuit.

   • No current flows through the branch with the capacitor.

2. Simplify the Circuit:

   • Ignore the branch containing the capacitor.

   • The circuit is now a simple series or parallel resistor combination (depending on the configuration).

3. Analyze the Resistors:

   • If R1 and R2​ are in series, calculate the equivalent resistance: Req=R1+R2​

   • If R1​ and R2 are in parallel: Req=(R1R2)/ (R1+R2)

4. Find Current and Voltage:

   • Total current from the source: I=V Req

   • Voltage across each resistor can be calculated using V=IR.

5. Voltage Across the Capacitor:

   • In steady state, the voltage across the capacitor equals the voltage across R2(if in parallel).

---

Key Tips

• In steady state, always treat the capacitor as an open circuit for DC analysis.

• Use equivalent resistance calculations to simplify complex resistor networks.

• Double-check connections (series or parallel) before simplifying the circuit.